研究メンバー
教授 田中 俊二 (Shunji Tanaka)
准教授 柳川 佳也 (Yoshinari Yanagawa)
助教 川本 卓樹 (Takaki Kawamoto)
研究室Webサイト: https://prodlab.sys.okayama-u.ac.jp
オペレーションズ・リサーチによる課題解決
オペレーションズ・リサーチとは,現実的課題に対してよりよい意思決定を行うための数理的・科学的手法の総称で,数理最適化,確率統計,データサイエンスなど,様々な分野にまたがります.本研究室ではオペレーションズ・リサーチの中で,とくに数理システム最適化を扱っています.数理システム最適化は,対象とするシステムの振る舞いを数理的アプローチによって最適化する学問です.本研究では,数理システム最適化を,おもに生産物流システムにおける諸問題に適用する研究を行っています.
スケジューリング問題
スケジューリング問題は,工場における生産スケジュール,鉄道の運行スケジュール,看護師の勤務スケジュールなど,種々のスケジュールを作成する問題です.本研究室では,機械を使って仕事を処理する際の作業スケジュールを作成する問題(機械スケジューリング)や,チームの対戦スケジュールを作成する問題(スポーツスケジューリング問題)などを対象として,最適なスケジュールを効率よく求めるためのアルゴリズムの研究を行っています.
(図1) 駐車場での待機を考慮した集配センターでの荷降ろし作業スケジューリング
(図2) 作業スケジュールの例
物流における積み込み・積み替え・整列問題
下の箱詰め問題の例にもある通り,限られたスペースに多くの荷物を保管しようとすると,3次元的に積み上げることになります.とはいえ,下の方に積んだ荷物はすぐには取り出せないので,取り出す順序を考えて積んだり(積み込み問題),手の空いているときに取り出しやすいよう積み直したり(整列問題),取り出しの妨げとなっている荷物の積み替え先を考えたり(積み替え問題),といったことが重要になってきます.本研究室では,これら積み込み,整列,積み替えに関する問題を数理モデル化するとともに,最適な計画を効率よく求めるためのアルゴリズムの研究を行っています.
(図3) コンテナターミナルに積まれたコンテナ

(図4) コンテナを番号順に取り出す問題(積み替え問題)の例
配達作業を効率化する積み付け法(箱詰め問題)
箱詰め問題は限られたスペースをいかに有効に使うかという良く知られた問題ですが、宅配における配達作業では、荷物をどのように積み付けるかによって、積み下ろし時の手数が大きく変わることが知られています。人による積み付け作業では経験の有無で結果が大きく異なるので、コンピュータによる積み付け案の提示が期待されていますが、小型の宅配車は荷物の取り出し口も2方向あるため問題は複雑であり、未熟な作業者が一般的な箱詰めルールで積み付けると、荷物スペース内に荷物が収まらなくなる場合が頻繁に生じます。そこで、荷物の位置関係を有向グラフを用いて表すことで荷物スペース内に荷物を積み付けて、積み下ろし手数をも削減する研究を行っています。
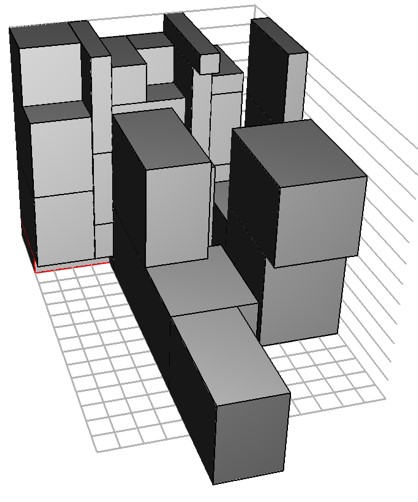
(図5) DBL法により積み付けた結果。荷物スペース内に収まりきらず、配送に適さない結果となった図。
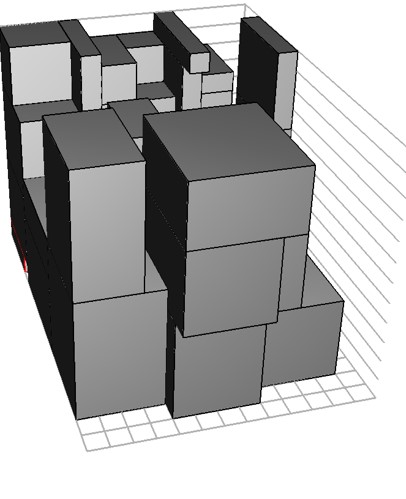
(図6) 荷物の位置関係を有向グラフで表し、グラフを変更することで荷物スペースの制約と積み下ろし手数とを考慮した積み付けにより、スペース内へ積み付けることができた図。
